5.1 排序算法
各种排序算法的时间复杂度以及稳定性

- 算法稳定性:在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的
1.冒泡排序
- 算法原理:相邻的数据进行两两比较,小(大)数放在前面,大(小)数放在后面,这样一趟下来,最小(大)的数就被排在了第一位,第二趟也是如此,如此类推,直到所有的数据排序完成。
- 时间复杂度:最坏:O(n2) 最好: O(n) 平均: O(n2) 空间复杂度:O(1) 稳定性:稳定。
/**
* 冒泡排序(升序排列)
* @param array
*/
public void bubbleSort(int[] a){
int len = a.length;
for(int i = 0 ; i < len ; i ++){
for(int j = 1 ; j < len ; j ++){
if(a[j-1] > a[j]){
int temp = a[j-1];
a[j-1] = a[j];
a[j] = temp;
}
}
}
}
2.选择排序
算法原理:
先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
- 时间复杂度:最坏:O(n2) 最好: O(n) 平均: O(n2) 空间复杂度:O(1) 稳定性: 稳定
/**
* 选择排序(升序排列)
* @param array
*/
public void selectSort(int[] a){
int len = a.length;
for(int i = 0 ; i < len ; i ++){
int flag = i;
for(int j = i+1 ; j < len ; j ++){
if(a[j] < a[flag]){
flag = j;
}
}
if(i != flag){
int temp = a[i];
a[i] = a[flag];
a[flag] = temp;
}
}
}
3.直接插入排序
- 算法原理: 每次将一个待排序的数据按照其关键字的大小插入到前面已经排序好的数据中的适当位置,直到全部数据排序完成。
时间复杂度:最坏:O(n2) 最好: O(n) 平均: O(n2) 空间复杂度:O(1) 稳定性: 稳定
排序演示:
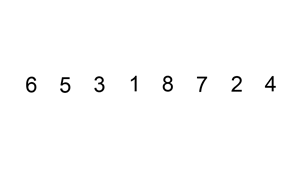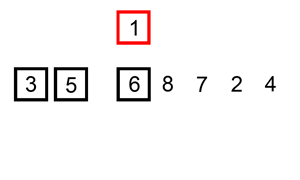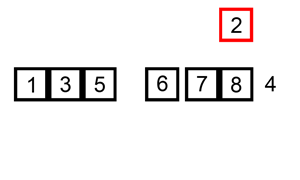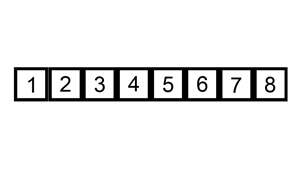
/**
* 直接插入排序(升序排列)
* @param array
*/
public void insertSort(int[] a){
int len = a.length;
for(int i = 1 ; i < len ; i ++){
int temp = a[i],j;
for(j = i ; j > 0 && a[j-1] > temp; j --){
a[j] = a[j-1];
}
a[j] = temp;
}
}
4.快速排序
- 算法原理:
- 从数列中挑出一个元素作为基准数。
- 分区过程,将比基准数大的放到右边,小于或等于它的数都放到左边。
- 再对左右区间递归执行第二步,直至各区间只有一个数。
时间复杂度:最坏:O(n2) 最好: O(nlogn) 平均: O(nlogn) 空间复杂度:O(logn) 稳定性: 不稳定
排序演示:
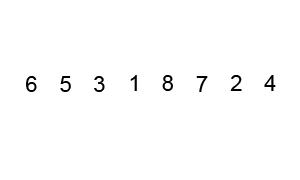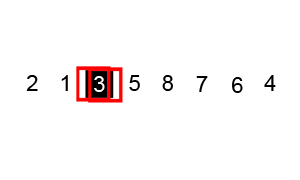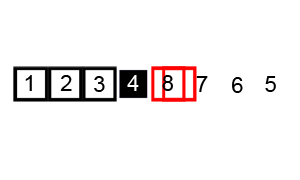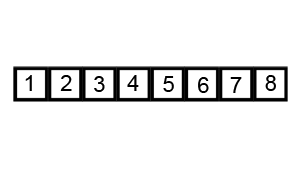
/**
* 快速排序-固定基准点(升序排列)
* @param array
*/
public void quickSort(int[] a,int l, int r){
if(l >= r) return;
int i = l , j = r;
while(i < j){
while(i < j && a[j] > a[l]) j -- ;
while(i < j && a[i] < a[l]) i ++ ;
if(i < j) swap(a, i, j);
}
if(i != l) swap(a, i, l);
quickSort(a, l, i-1);
quickSort(a, i+1, r);
}
快排的最差情况为序列完全有序,此时快排退化为冒泡排序,时间复杂度为 O(n2)。
- 快排的优化
- 随机选取基准
/**
* 快速排序-随机基准点(升序排列)
* @param array
*/
public void quickSort(int[] a,int l, int r){
if(l >= r) return;
int i = l , j = r;
Random rand = new Random();
int flag = l + rand.nextInt(r-l+1);
swap(a, l, flag);
while(i < j){
while(i < j && a[j] > a[l]) j -- ;
while(i < j && a[i] < a[l]) i ++ ;
if(i < j) swap(a, i, j);
}
if(i != l) swap(a, i, l);
quickSort(a, l, i-1);
quickSort(a, i+1, r);
}
public void swap(int[]a , int i , int j){
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
5.归并排序
- 算法原理:将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。
- 时间复杂度:最坏:O(nlogn) 最好: O(n) 平均: O(nlogn) 空间复杂度:O(1) 稳定性: 稳定
- 排序演示:

/**
* 归并排序(升序排列)
* @param array
*/
public static void mergeSort(int[] a,int start,int end){
if(start+1 >= end)return;
int mid = (start+end)/2;
mergeSort(a, start, mid);
mergeSort(a, mid, end);
merge(a,start,end);
}
public static void merge(int[] a,int start,int end){
int b[] = new int[a.length];
int mid = (start + end)/2;
int i = start, j = mid,k = start;
while(i < mid && j < end){
if(a[i] < a[j])b[k++] = a[i++];
else b[k++] = a[j++];
}
while(i < mid) b[k++] = a[i++];
while(j < end) b[k++] = a[j++];
while(start < end)a[start] = b[start++];
}
6.堆排序
算法原理:堆排序就是把最大堆堆顶的最大数取出,将剩余的堆继续调整为最大堆,再次将堆顶的最大数取出,这个过程持续到剩余数只有一个时结束。
时间复杂度:最坏:O(nlogn) 最好: O(nlogn) 平均: O(nlogn) 空间复杂度:O(1) 稳定性: 不稳定
/**
* 堆排序(升序排列)-建立最大堆
* @param array
*/
public static void heapSortAsc(int[] a){
int len = a.length;
for(int i = len/2 - 1 ; i >= 0 ;i --){
maxHeapDown(a,i,len-1);
}
for(int i = len - 1 ; i > 0 ; i --){//堆顶和末尾交换
swap(a, i, 0);
maxHeapDown(a, 0, i-1);
}
}
public static void maxHeapDown(int[]a , int start , int end){//调整成为最大堆
int son = start*2 + 1;//左儿子
int root = a[start];
for(; son <= end ;start = son,son = 2*son+1){
if(son < end && a[son] < a[son + 1]){
son ++;//右儿子
}
if(root >= a[son])break;
else {
swap(a, start, son);
}
}
}